
Kreisumfang berechnen mit dem praktischen Rechner
Den Kreisumfang zu berechnen, fällt nicht nur vielen Schülern, sondern auch Erwachsenen schwer. Mit unserem Tool gestaltet sich die Kreisberechnung jedoch spielend einfach, egal ob Sie den Kreisumfang, den Radius, den Durchmesser oder den Flächeninhalt des Kreises bestimmen möchten.
Berechnen Sie hier den Kreisumfang
Nachfolgend einige Beispiele zur Berechnung des Kreisumfangs:
Sofern Sie mit dem Radius rechnen möchten, klicken Sie die Option „Radius“ an. Wir geben anschließend einen Beispielwert von 15 ein.

Um das Ergebnis zu erhalten, klicken wir auf die Schaltfläche berechnen, sodass Folgendes angezeigt wird:

Bei einem Radius von 15, hat der Kreis somit einen Durchmesser von 30, einen Umfang von 94,247779607694 (gerundet 94,25) und einen Flächeninhalt von 706,8583470577 (gerundet 706,86)
Zur Ermittlung des Durchmessers eines Kreises, klicken wir die Option „Durchmesser“ an und geben ebenfalls einen entsprechenden Wert an. Wir bleiben bei einem Wert von 15.

Es erscheint folgendes Ergebnis:
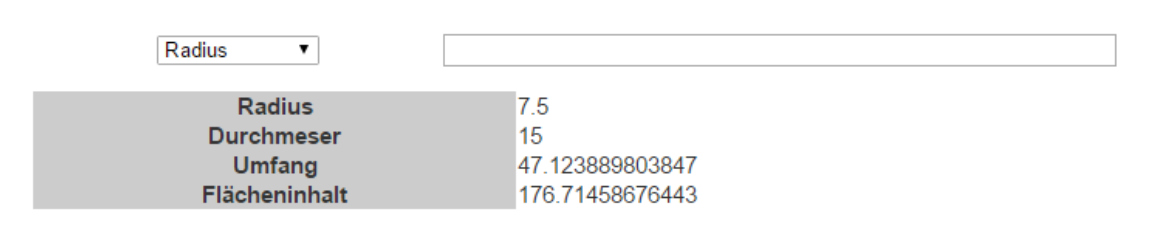
Bei einem Durchmesser von 15, erhalten wir einen Radius von 7,5, einen Umfang von 42,123889903847 (gerundet 42,12) sowie einen Flächeninhalt von 176,71458676443 (gerundet 176,71).
Wenn Sie den Umfang berechnen möchten, wählen Sie die Option „Umfang“ und geben Sie den Wert an, der in unserem Beispiel wieder bei 15 liegt.

Das Ergebnis gestaltet sich folgendermaßen:

Bei einem Umfang von 15, erhalten Sie eine Radius von 2,3873241463784 (gerundet 2,39), einen Durchmesser von 4,7746482927569 (gerundet 4,77) sowie einen Flächeninhalt von 17,904931097838 (gerundet 17,90).
Als letztes berechnen wir den Flächeninhalt des Kreises, ebenfalls mit 15, nachdem wir die Option „Flächeninhalt“ gewählt haben.

Es erscheint folgendes Ergebnis:
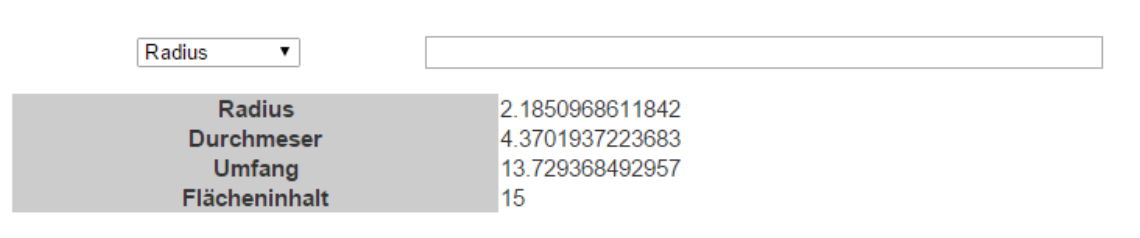
Berechnungen in der Geometrie
Vielen Schülern, aber auch Erwachsene fallen Berechnungen in der Geometrie nicht leicht, was in erster Linie damit zu begründen ist, dass es sich oft um komplexe Gleichungen handelt, die angewendet werden müssen. Schließlich kann man nicht nur die Kreisberechnung durchführen, sondern beispielsweise auch die Dreiecksberechnung. Auch die Werte für Vielecke (Polygone) oder das Zwölfeck können auf komplexe Weise ermittelt werden.
Damit Ihnen zumindest die Ermittlung vom Kreisumfang ohne Anwendung einer schwierigen Gleichung gelingt, können Sie unseren Rechner zur Hilfe nehmen.
Was ist ein Kreis?
Bei einem Kreis handelt es sich um eine geometrische Figur, welche nicht nur über einen Kreisring, sondern auch über eine Kreisfläche verfügt. Wie groß der jeweilige Kreisbogen (bei dem es sich um die zusammenhängende Linie handelt) ist, können Sie mit unserem praktischen Rechner ermitteln. Des Weiteren berechnen Sie problemlos einen beliebigen Kreisausschnitt.
Der Kreis verfügt über einen Außen- sowie Inkreis. Werden zwei Punkte auf der Kreislinie miteinander verbunden, spricht man hierbei von der Kreissehne.
Bei der Berechnung von Kreisausschnitt oder Kreisfläche kommen auch Begriffe wie „Sekante“, „Tangente“ und „Passante“ zum Einsatz. Wenn der Abstand zwischen dem Mittelpunkt des Kreises und der Geraden geringer als der Kreisradius ist, bezeichnet man dies als Sekanten. Tangenten sind es wiederum, wenn der Abstand des Kreismittelpunktes zur Geraden mit dem Radius übereinstimmen und sich hierdurch ein gemeinsamer Punkt ergibt. Ist der Abstand des Mittelpunktes des Kreises von der Geraden größer als der Radius des Kreises, und haben Kreis und Gerade somit keinerlei gemeinsamen Punkt, bezeichnet man dies als Tangente.
Ist von einem Kreissektor, der auch als „Kreisabschnitt“ bezeichnet wird, die Rede, meint man eine Fläche, die von zwei Radien begrenzt wird, zwischen denen sich ein Kreisbogen befindet.
Die Kreiszahl wiederum definiert den Umfang eines Kreises im Verhältnis zu seinem Durchmesser. Wir kennen diese Kreiszahl unter dem Begriff Pi, die den Wert 3,1415926… hat. Den Durchbruch hinsichtlich der Kreisberechnung haben wir definitiv Archimedes, einem griechischen Mathematiker, Physiker und Ingenieur zu verdanken, welcher die Zahl Pi ermittelt hat. Gelungen ist ihm dies mit dem sogenannten Näherungsverfahren. Die Zahl Pi wird bei der Kreisberechnung in der Regel auf zwei Nachkommastellen gekürzt.
(Quelle: Wikipedia)
Was ist die Elementargeometrie?
Als Elementargeometrie wird die Form der Geometrie benannt, die den Schülern im Schulunterricht beigebracht wird. In der Regel wird dieses Fach in Kombination mit Mathe gelehrt, da man beispielsweise für die Berechnung der Eckenzahl der Vielecke rechnen muss. Auch die Berechnung vom Dreieck wird den Schülern im Unterricht beigebracht. Diesbezüglich spielt der Satz des Pythagoras eine beträchtliche Rolle.
Die Kurvendiskussion ist ebenfalls eine Kombination aus Geometrie und Mathematik, welche jedoch erst in den höheren Schulklassen gelehrt wird. Des Weiteren erfahren die Schüler, worum es sich beim sogenannten „Einheitskreis“ handelt und was ein Strahlensatz ist. Mit Letzterem können Längen gewisser Strecken berechnet werden.
Im Fach Mathe geht es hingegen nicht um die Berechnung geometrischer Flächen, sondern beispielsweise um den Dreisatz, die Umrechnung von Maßeinheiten, die Zinsrechnung, die Exponentialfunktion sowie um die lineare und die quadratische Gleichung. Auch zur Berechnung dieser Dinge können Sie verschiedene Online Tools nutzen.
Wie wird der Umfang eines Kreises berechnet?
Der Kreis hat einen Mittelpunkt, von dem aus die Entfernung zur Kreislinie immer gleich ist. Hierbei handelt es sich um den Radius „r“. Des Weiteren verfügt der Kreis über den Durchmesser, der doppelt so groß ist, wie der Radius. Zur Berechnung benötigen wir des Weiteren die Kreiszahl Pi (π).
Mit diesen Formeln wird der Kreisumfang berechnet:
U = 2 x π x r
Oder
U = π x d
Bei „U“ handelt es sich um den Umfang des Kreises, welcher in Meter angegeben wird.
π hat einen Wert von 3,14159
Der Radius „r“ wird ebenfalls in Metern angegeben, sowie der Durchmesser „D“.
Anhand des obigen Beispiels zur Berechnung des Umfangs ergibt sich folgende Berechnung: (Der Radius beträgt 15 Meter)
U = 2 x π x r
U = 2 x π x 15m
U = 94,2477 (gerundet 94,25)